La résolution des équations du troisième degré est assez complexe car on ne connaît aucune formule donnant directement les trois éventuelles solutions, contrairement au second degré. Toutefois, on en connaît une donnant une solution (voir plus bas). Une autre difficulté vient du fait que pour résoudre ces équations, il a fallu attendre l'apparition des nombres complexes. Il est donc utile, pour les résoudre, de savoir manipuler les complexes (programme de terminale).
La première étape consiste à trouver une solution de l'équation. Bien souvent, le mieux est de trouver une « solution évidente » : une solution souvent simple, 0, 1, 2 ou -1 par exemple. Ainsi, l'équation x3 + 2x2 - 5x + 2 = 0 admet 1 comme solution évidente. Si on ne trouve pas de solution évidente, on pourra utiliser la formule ci-dessous. Si l'équation n'est pas du type demandé par cette formule, il faut la modifier. Si votre équation commence par « x3 + mx2 + ... », notez « x = y - m/3 », remplacez dans l'équation et développez. Les x2 vont disparaître et vous pourrez appliquer la formule ci-dessous pour avoir une première solution.
Une fois une solution « a » trouvée, on peut factoriser le polynôme par (x-a). Pour cela, développez l'expression « (x-a)(x2 + bx + c) », et identifiez les coefficients que vous trouvez à ceux de l'équation du troisième degré. Ainsi, on se ramène à une équation du second degré qu'il est simple de résoudre.
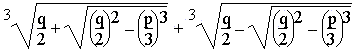Quelle est donc cette formule dont je vous parle depuis cinq minutes ? Cette formule est dite de Tartaglia-Cardan, mais certains pensent que Cardan l'a demandée à Tartaglia pour la publier sous son nom. Cette formule permet de trouver une solution particulière aux équations de la forme : x3 = px + q. La solution est donnée par la formule ci-contre. On notera que si les nombres sous les racines sont négatifs, on utilisera les notations complexes, la formule restant alors valable.
La démonstration n'est pas très difficile, mais ne peut être écrite en format html à cause des nombreux symboles mathématiques. C'est pourquoi je vous propose de la télécharger en format PDF, compressé avec Microsoft Winzip : formuletartacardan.zip, 52 Ko (si vous ne possédez pas le logiciel Acrobat Reader ou Winzip, allez sur la page de liens).
Exemple de résolution :
On veut résoudre l'équation 2x3 + 12x2 - 96x - 602 = 0.
1) On se ramène à une équation de la forme de la formule de Tartaglia-Cardan : on doit d'abord avoir le coefficient 1 devant x3 donc on divise l'équation par 2 : x3 + 6x2 - 48x - 301 = 0. On a un membre x2 avec comme coefficient 6. On pose donc x = y - 6/3, soit x = y - 2. Alors (y-2)3 + 6(y-2)2 - 48(y-2) - 301 = 0, soit en développant et en simplifiant : y3 = 60y + 189.
2) On utilise la formule de Tartaglia-Cardan : on a ici p = 60 et q = 189. La formule donne donc la solution y = (189/2 + racine((189/2)2-(60/3)3))1/3 + (189/2 - racine((189/2)2-(60/3)3))1/3 = (94,5 + racine(94,52 - 203))1/3 + (94,5 - racine(94,52 - 203))1/3 = (94,5 + racine(8930,25 - 8000))1/3 + (94,5 - racine(8930,25 - 8000))1/3 = (94,5 + racine(930,25))1/3 + (94,5 - racine(930,25))1/3 = (94,5 + 30,5)1/3 + (94,5 - 30,5)1/3 = 1251/3 + 641/3 = 5 + 4 = 9. On peut d'ailleurs vérifier que 93 - 60x9 - 189 = 729 - 540 - 189 = 0. 9 est donc bien solution de l'équation en y.
3) On factorise : on doit avoir y3 - 60y - 189 = (y-9)(y2 + by + c). En développant le côté droit, on obtient y3 - 60y - 189 = y3 + (b-9)y2 + (c-9b)y - 9c. Dès lors, on doit avoir (b-9) = 0, c-9b = -60 et -9c = -189. Finalement, b = 9 et c = 21, soit y3 - 60y - 189 = (y-9)(y2+9y+21).
4) On a une équation du second degré, qu'on résout comme d'habitude avec le discriminant : les deux autres solutions sont données par y2+9y+21 = 0, équation de discriminant 92 - 4x1x21 = -3. D'où deux solutions complexes : (-9 + i.racine(3))/2 et (-9 - i.racine(3))/2.
5) On conclut : y est donc dans l'ensemble {-4,5 + i.racine(3)/2 ; -4,5 - i.racine(3)/2 ; 9}. Or x = y - 2, donc les solutions de l'équation de départ sont {-6,5 + i.racine(3)/2 ; -6,5 - i.racine(3)/2 ; 7} (vous pouvez vérifier...).