La manière que nous avons de poser la multiplication de deux nombres n'est pas la seule. Voyons une autre façon de le faire. Nous allons traiter l'exemple de 321 x 512.
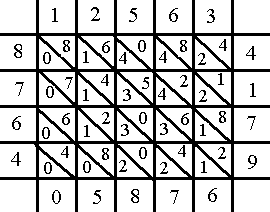
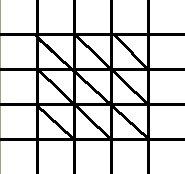Dans un premier temps, on trace un tableau comme ci-contre. Comme la multiplication implique deux nombres de 3 chiffres, on met 5 lignes et 5 colonnes. S'il y avait eu un nombre de 2 chiffres et un de 6, il aurait fallu 4 lignes et 8 colonnes (ou l'inverse, ça n'a aucune importance). A l'intérieur des cases qui ne sont pas sur les lignes et colonnes extérieures, on trace des diagonales dirigées du haut à gauche vers le bas à droite.
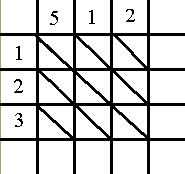On entre les deux nombres à multiplier. L'un est à gauche, écrit de bas en haut et l'autre est en haut, écrit de gauche à droite.
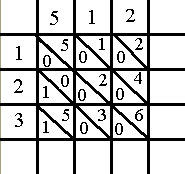Dans les cases centrales, on entre les produits des chiffres de la ligne et de la colonne. Dans la partie basse-gauche, on entre le chiffre des dizaines, dans la partie haute-droite, on entre le chiffre des unités. Par exemple, dans la case centrale la plus en haut à gauche, on entre le produit de 1 (ligne) et 5 (colonne) soit 5 ou 05 (en effet, si le chiffre est inférieur à 10, on rajoute 0 pour les dizaines). On place le 0 dans la partie de la case la plus basse et le 5 dans la partie la plus haute.
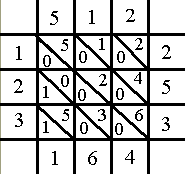On fait les sommes en suivant les diagonales et en commençant par en haut à droite. Ici, on met 2 dans la case extérieure en haut à droite. Pour la case en dessous, on fait 1 + 0 + 4 = 5. Dans la case suivante, 5 + 0 + 2 + 0 + 6 = 13. On inscrit donc 3 et on rajoute une retenue de 1 dans la case suivante (qui est la plus à droite de la ligne du bas) : 1 (retenue) + 0 + 0 + 0 + 3 + 0 = 4. On continue de même, la case suivante étant à gauche.
Le résultat se lit en commençant par le bas (de gauche à droite) puis à droite (de bas en haut) : 164 352.
Voici un autre exemple pour mieux comprendre :
4678 x 12563 = 58 769 714
Cette méthode peut vous sembler difficile mais avec un peu d'entraînement, elle deviendra vite naturelle. Appelée multiplication par jalousies, elle était utilisée au Moyen-Age en Chine, Inde et dans les pays arabes. Elle se pratique encore en Turquie. Son nom vient du fait que les diagonales tracées rappellent la structure de certaines fenêtres orientales appelées jalousies.
Je la préfère à celle qu'on apprend à l'école. En effet, avec cette dernière, on a besoin des retenues lorsqu'on fait les multiplications ligne par ligne puis lorsqu'on additionne. Avec la multiplication par jalousies, on n'a besoin des retenues seulement lors des additions de la dernière étape. Or, les petits ayant souvent du mal avec les retenues, il leur serait à mes yeux plus facile d'utiliser la méthode par jalousies. Mais c'est vrai qu'elle est un peu plus longue, même quand on la maîtrise bien.
Source :
Les nombres et leurs mystères, André Warusfel, éditions du Seuil, 1961