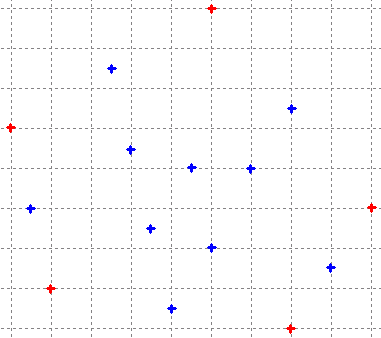
Sur un plan quadrillé, on choisit cinq points sur les sommets du quadrillage (ci-contre en rouge). On a alors dix couples de points rouges (Si on les note ABCDE, on a les couples AB, AC, AD, AE, BC, BD, BE, CD, CE, DE), ce qui définit dix milieux (en bleu). Sauriez-vous dire pourquoi quels que soient les cinq points de départ, un milieu au moins tombe sur le quadrillage ?
Munissons notre plan d'un repère suivant le quadrillage, de manière à ce que les lignes et colonnes tracées donnent des coordonnées entières aux points. (Autrement dit, le point en bas à gauche est l'origine (0,0), celui à sa droite est (1,0) et celui au dessus est (0,1)).
Quand on choisit un point, il appartient à l'une des quatre familles ci-dessous :
- les points d'abscisse et d'ordonnée paires
- les points d'abscisse paire et d'ordonnée impaire
- les points d'abscisse impaire et d'ordonnée paire
- les points d'abscisse et d'ordonnée impaires
Ici, on a choisi cinq points rouges. Alors, forcément deux au moins vont se retrouver dans la même famille (car il y a 5 points et 4 familles, donc pas assez de familles pour que chaque points soit séparé de tous les autres - c'est ce qu'on appelle le principe des tiroirs).
Alors pour ces deux points, comme leurs abscisses x1 et x2 sont de même parité, l'abscisse de leur milieu (la moyenne de x1 et x2) est un nombre entier. De même, l'ordonnée du milieu est un nombre entier. Et alors ce milieu est exactement sur le quadrillage !
Bien entendu, avec seulement 4 points, il est possible de s'arranger pour avoir tous les milieux hors du quadrillage : il suffit de prendre un point dans chaque famille !
Source :
Maths et malices n°13, ACL éditions, septembre-octobre 1993