De tous temps, les hommes ont voulu avoir des moyens de communiquer secrètement : à but militaire (on citera le célèbre code de César, consistant à décaler l'alphabet), ou civil (protection de données sur Internet, sécurité des cartes bancaires, ...). De ce désir est née la cryptographie, l'art de coder les messages.
Dans les années 1970, l'armée américaine a besoin d'un nouvel algorithme de cryptage. Le Bureau Fédéral des Standards lance alors un concours pour trouver cet algorithme. C'est IBM qui se place en première position, avec un algorithme original (et au doux nom) : Lucifer.
Cet algorithme est accepté par le Bureau Fédéral mais nécessite quelques améliorations : son successeur sera finalement approuvé en 1977, il s'agit du DES.
Le Data Encryption Standard (standard de codage des données) est un algorithme à clé secrète : sa sécurité ne réside pas dans son fonctionnement, connu de tous, mais dans le choix d'une clé, servant à coder et décoder, que se partagent les correspondants. En l'occurrence, la clé du DES est une clé de 64 bits, ce qui signifie qu'elle est une suite de 64 chiffres, 0 ou 1 (note : certains disent que la clé ne contient que 56 bits. En effet, 56 bits sont choisis par l'utilisateur, les 8 autres sont calculés à partir des 56). Voyons comment il fonctionne.
Le DES agit sur des blocs de 64 bits, ou 8 octets. Les textes plus longs doivent donc être découpés en blocs de 64. Une fois les blocs obtenus, chacun subit l'algorithme du DES. L'algorithme consiste en fait en 16 itérations d'un cycle, chaque étape 1 à 16 ne différant que par la clé qu'on utilise (voir plus bas : génération des clés).
Permutation initiale
Les bits du tableau sont échangés selon la table suivante : le bit 58 est passé en position 1, le bit 50 vient en position 2, et on continue jusqu'au bit 7 qui se place en dernière position.
| 58 | 50 | 42 | 34 | 26 | 18 | 10 | 2 |
| 60 | 52 | 44 | 36 | 28 | 20 | 12 | 4 |
| 62 | 54 | 46 | 38 | 30 | 22 | 14 | 6 |
| 64 | 56 | 48 | 40 | 32 | 24 | 16 | 8 |
| 57 | 49 | 41 | 33 | 25 | 17 | 9 | 1 |
| 59 | 51 | 43 | 35 | 27 | 19 | 11 | 3 |
| 61 | 53 | 45 | 37 | 29 | 21 | 13 | 5 |
| 63 | 55 | 47 | 39 | 31 | 23 | 15 | 7 |
Le tableau obtenu est alors coupé en deux blocs : le bloc de gauche, qui contient les 32 premiers bits, et le bloc de droite, qui contient les 32 derniers. On notera d'ailleurs, en observant la table précédente, que la partie gauche (notée G0) contient les bits dont la position initiale était paire, et la partie droite (D0) contient les bits de position initiale impaire.
Le cycle
Pour chaque cycle numéroté i (i variant de 1 à 16), nous partons avec Gi-1 et Di-1 (les parties gauches et droites fournies par le cycle précédent).
On garde pour l'instant la partie gauche intacte. On va transformer la partie droite pour l'étendre de 32 bits à 48 bits. Pour cela, on va simplement répéter certains bits. On utilise la table suivante :
| 32 | 1 | 2 | 3 | 4 | 5 |
| 4 | 5 | 6 | 7 | 8 | 9 |
| 8 | 9 | 10 | 11 | 12 | 13 |
| 12 | 13 | 14 | 15 | 16 | 17 |
| 16 | 17 | 18 | 19 | 20 | 21 |
| 20 | 21 | 22 | 23 | 24 | 25 |
| 24 | 25 | 26 | 27 | 28 | 29 |
| 28 | 29 | 30 | 31 | 32 | 1 |
En clair, le nouveau texte est constitué des bits 32, 1, 2, 3, etc... Certains bits sont répétés, d'où les 16 bits supplémentaires. Le résultat obtenu est noté E(Di-1), E pour extension.
Nous allons maintenant faire intervenir la clé Ki (voir plus bas pour la création de cette clé), qui contient elle aussi 48 bits. Nous allons simplement la mixer avec les bits précédemment obtenus. Pour ce faire, on utilise la fonction OU EXCLUSIF. « A OUEX B » est vrai si et seulement si une seule des expressions A et B est vraie. Avec des 0 et des 1, a ouex b est la somme de a et b, avec un modulo 2 (donc 1 ouex 1 = 0 ; 0 ouex 1 = 1 ; 1 ouex 0 = 1 ; 1 ouex 1 = 0). Le résultat obtenu est noté Ki + E(Di-1).
Nous avons à présent un tableau de 48 bits. Nous allons en faire un tableau de 32 bits. La première chose à faire est de découper notre tableau en 8 tableaux contenant chacun 6 bits. Puis chaque groupe de 6 bits va être transformé en groupe de 4 bits. (8 x 4 = 32 !). La transformation se fait grâce à la table de substitution ci-dessous. Elle contient huit petites tables numérotées de 1 à 8. Chacune est composée de 16 colonnes (numérotées de 0 à 15) et 4 lignes (0 à 3). A chaque intersection, on trouve un nombre entre 0 à 15.
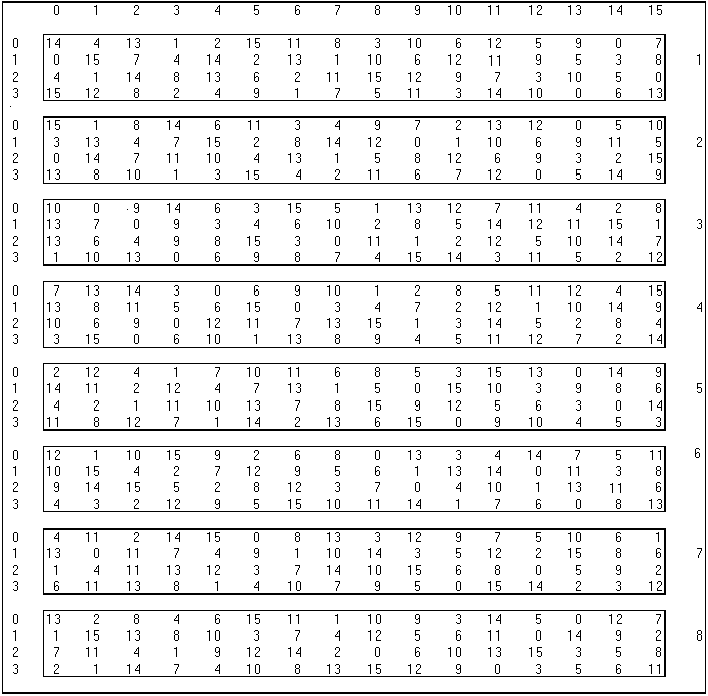Le secret de cette table réside dans le code binaire. Nous devons transformer 8 groupe de 6 bits. Pour chaque groupe, on va utiliser la petite table ayant le même numéro. On considère alors le premier et le dernier bits. Ils sont deux et correspondent donc en binaire à un chiffre compris entre 0 et 3 : ce chiffre nous donne le numéro de la ligne à utiliser. Les quatre autres bits correspondent à un nombre compris entre 0 et 15, et nous donnent donc la colonne à utiliser. A l'intersection de la ligne et de la colonne, on a un nombre plus petit que 16, on peut donc le traduire en binaire, en utilisant seulement 4 chiffres.
Pour plus d'explications si vous n'avez pas compris cette étape, cliquez ici.
Le résultat obtenu est noté S(Ki + E(Di-1)), S pour substitution.
Les 32 bits obtenus vont être permutés, comme à l'étape 1, avec la table suivante :
| 16 | 7 | 20 | 21 |
| 29 | 12 | 28 | 17 |
| 1 | 15 | 23 | 26 |
| 5 | 18 | 31 | 10 |
| 2 | 8 | 24 | 14 |
| 32 | 27 | 3 | 9 |
| 19 | 13 | 30 | 6 |
| 22 | 11 | 4 | 25 |
On obtient alors un tableau : P(S(Ki + E(Di-1))), P pour permutation. Pour plus de simplicité, on le notera à présent D'i-1
A présent, nous avons fait intervenir la partie droite initiale et la clé, mais la partie gauche est restée intacte. Pour finir le cycle :
- On mixe la partie gauche initiale, avec les 32 bits transformés, en utilisant là encore la fonction OU EXCLUSIF.
- Le résultat obtenu, qui contient donc 32 bits, forme la partie droite du nouveau tableau.
- A gauche, on accole la partie droite initiale.
On a alors obtenu un tableau de 64 bits.
Finalement, Gi = Di-1 et Di = D'i-1 + Gi-1
Permutation inverse
Une fois les seize cycles effectuées, on a obtenu G16 et D16. On inverse alors les deux moitiés du résultat et on réalise une dernière permutation :
| 40 | 8 | 48 | 16 | 56 | 24 | 64 | 32 |
| 39 | 7 | 47 | 15 | 55 | 23 | 63 | 31 |
| 38 | 6 | 46 | 14 | 54 | 22 | 62 | 30 |
| 37 | 5 | 45 | 13 | 53 | 21 | 61 | 29 |
| 36 | 4 | 44 | 12 | 52 | 20 | 60 | 28 |
| 35 | 3 | 43 | 11 | 51 | 19 | 59 | 27 |
| 34 | 2 | 42 | 10 | 50 | 18 | 58 | 26 |
| 33 | 1 | 41 | 9 | 49 | 17 | 57 | 25 |
L'algorithme du DES est alors terminé.
Formation des clés :
Comment obtient-on les 16 clés Ki de 48 bits à partir de la clé de 64 bits donnée par l'utilisateur ?
Tout d'abord, on fait une première permutation pour passer à 56 bits, et on en profite pour séparer au passage la partie gauche et la partie droite :
| G: | 57 | 49 | 41 | 33 | 25 | 17 | 9 | D: | 63 | 55 | 47 | 39 | 31 | 23 | 15 |
| 1 | 58 | 50 | 42 | 34 | 26 | 18 | 7 | 62 | 54 | 46 | 38 | 30 | 22 | ||
| 10 | 2 | 59 | 51 | 43 | 35 | 27 | 14 | 6 | 61 | 53 | 45 | 37 | 29 | ||
| 19 | 11 | 3 | 60 | 52 | 44 | 36 | 21 | 13 | 5 | 28 | 20 | 12 | 4 |
Ensuite, on décale les bits de chaque partie (gauche et droite) vers la gauche. Le nombre de bits de décalage dépend du numéro du cycle, c'est pour cela que la clé est à chaque fois différente. Les décalages effectués sont, dans l'ordre des cycles : 1, 2, 4, 6, 8, 10, 12, 14, 15, 17, 19, 21, 23, 25, 27, 28.
Enfin, on recolle la gauche et la droite et on fait une autre permutation, en passant à 32 bits :
| 14 | 17 | 11 | 24 | 1 | 5 |
| 3 | 28 | 15 | 6 | 21 | 10 |
| 23 | 19 | 12 | 4 | 26 | 8 |
| 16 | 7 | 27 | 20 | 13 | 2 |
| 41 | 52 | 31 | 37 | 47 | 55 |
| 30 | 40 | 51 | 45 | 33 | 48 |
| 44 | 49 | 39 | 56 | 34 | 53 |
| 46 | 42 | 50 | 36 | 29 | 32 |
Et après ?
Et comment on décode ? On utilise exactement le même algorithme, mais en inversant l'ordre des clés : Le cycle 1 est fait avec la clé 16, le cycle 2 avec la clé 15, ... jusqu'au cycle 16 qui est fait avec la clé 1.
C'est bien beau tout ça, mais ça n'explique que comment on code une succession de bits, 0 ou 1. Comment code-t-on les textes ? En fait, c'est simple. On passe d'abord par le code ASCII (prononcer « aski »). Il fait correspondre à chaque caractère utilisé un nombre. Il existe deux ASCII. Le code ASCII standard a été créé dans les années 60 et contient 128 caractères, numérotés de 0 à 127. Il est universel, chaque machine a le même.
Cependant, le code standard est anglais. Il ne contient donc que les caractères anglais. Ce qui pose pas mal de problèmes : comment font les Français avec les accents ? Comment font les Espagnols avec les tildes ? On a donc développé plus tard le code ASCII étendu. Il contient 256 caractères, et augmente donc considérablement les possibilités.
La solution pour passer d'un texte à des bits est donc la suivante : on remplace d'abord chaque caractère par son numéro dans le code ASCII (standard ou étendu selon les cas), puis on remplace ce numéro par son équivalent en binaire, ce qui nous donne bien une succession de 0 et 1. Il y a juste un petit inconvénient. Contrairement au standard l'ASCII étendu n'est pas universel. Il varie selon les machines et les constructeurs. C'est pourquoi les algorithmes qui se basent dessus peuvent rencontrer des difficultés. Si vous codez un texte avec une machine, que vous passez le code à un ami et s'il n'a pas le même ASCII lorsqu'il décode, certains caractères seront modifiés. Cela dit, les caractères les plus courants (ponctuation, non accentués et chiffres) sont dans le standard.
J'ai écrit un programme qui permet de coder ou décoder un texte en utilisant le DES : voyez cette page.