Vous savez sûrement que les trois médiatrices des côtés d'un triangle se croisent en un point O appelé centre du cercle circonscrit. Mais savez-vous le prouver ? Voyez ce PDF (10 Ko - si vous n'avez pas le logiciel Acrobat Reader, voyez la page de liens), niveau troisième.
Pouvez-vous prouver que les trois hauteurs se coupent en un même point H appelé orthocentre ? Démonstration ici (12
Ko), niveau première.
Et pouvez-vous démontrer que les trois médianes sont concourantes en un point unique G, le centre de gravité ? Voici la réponse (16 Ko), niveau seconde.
Enfin, et c'est ici que ça devient intéressant, saviez-vous que ces trois points sont alignés (quand le triangle n'est pas équilatéral, et donc qu'ils ne sont pas confondus) et même que la longueur GH est le double de OG ? Voyez la démonstration ici (14 Ko), niveau terminale.
Pour visualiser ces propriétés, téléchargez ce programme : vous pourrez tracer des triangles et observer les trois points.
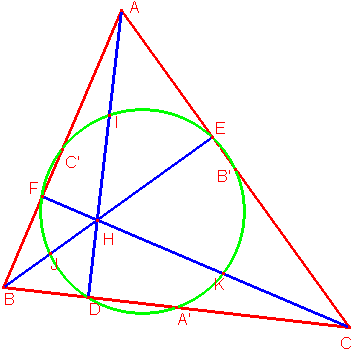La droite qui lie ces trois points est appelée droite d'Euler. Mais il y a aussi le cercle d'Euler : dans un triangle ABC (ci-contre en rouge) d'orthocentre H, les milieux A', B' et C' des segments [BC], [CA] et [AB], les pieds D, E et F des hauteurs issues de A, B et C et les milieux I, J et K des segments [AH], [BH] et [CH] (ci-contre, les hauteurs sont en bleu) sont situés sur un même cercle (en vert). Ce résultat est aussi nommé théorème des neuf cercles.
Pour démontrer ce résultat, il faut d'abord nous rappeler du théorème de Varignon (1731) : les milieux des côtés d'un quadrilatère sont les sommets d'un parallélogramme. Ceci se démontrer comme simple application de la relation de Chasles sur les vecteurs ou du théorème de Thalès.
En utilisant ce théorème dans le quadrilatère BAHC, C'IKA' est donc un paralélogramme. Or (BH) et (AC) sont perpendiculaires par définition d'une hauteur. Par application du théorème des milieux dans le triangle AHC, (IK) et (AC) sont parallèles, et on a la même chose pour (BH) et (C'I) (dans le triangle ABH). Dès lors, (C'I) et (IK) sont perpendiculaires donc C'IKA' est en fait un rectangle.
De même en raisonnant dans le quadrilatère CAHB, B'IJA' est un autre rectangle. Chacun d'eux est donc inscrit dans un cercle mais comme ils ont une diagonale commune, [IA'], ils sont en fait inscrit dans le même cercle, celui de diamètre [IA']. On notera O ce cercle. En utilisant nos deux rectangles, on obtient que [C'K] et [B'J] sont aussi des diamètres de O.
Par construction des hauteurs, les rectangles IDA', JEB' et KFC' sont rectangles, d'hypothénuses respectives [IA'], [JB'] et [KC'] qui sont des diamètres de O donc D, E et F sont également sur O. Finalement, A', B', C', D, E, F, I, J et K sont sur le même cercle O !
Source :
http://mathematiques4.free.fr