 Théorème d'Aubel
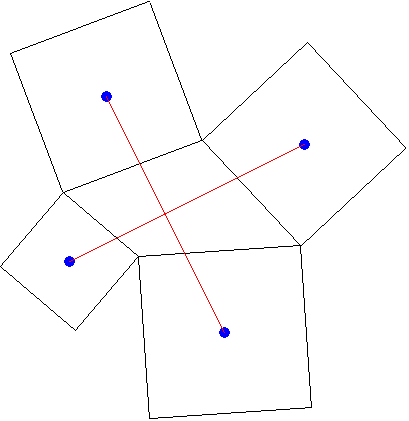
Théorème d'Aubel
A partir d'un quadrilatère quelconque, tracez les quatre carrés extérieurs au quadrilatère et qui ont pour côtés les côtés du quadrilatère. Prendre les centres de ces carrés. Si on relie chaque centre à celui du carré opposé, on obtient deux droites perpendiculaires et de même longueur.
 Théorème de Victor Thébault (1937)
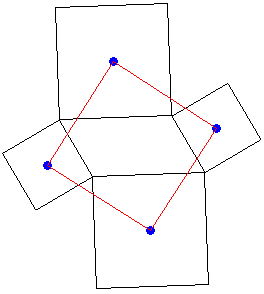
Théorème de Victor Thébault (1937)
C'est un cas particuliers du théorème d'Aubel. On remplace ici le quadrilatère quelconque par un parallélogramme (image 2). Dans ce cas, les quatre centres des carrés forment eux-mêmes un carré.
Ceci peut être vu comme le pendant dans un quadrilatère du théorème de Napoléon (résultat semblable dans un triangle).
Démonstrations :
Souvent en mathématiques, les cas particuliers sont plus simples à démontrer que les cas généraux. C'est ici le cas : Le théorème de Victor Thébault se démontre plus facilement car il ne nécessite que des connaissances de première (produits scalaires) alors que celui d'Aubel nécessite des connaissances de terminale, en spécialité mathématiques (similitudes directes). Il est aussi possible de démontrer ces théorèmes en même temps en utilisant les nombres complexes.
Vous pouvez télécharger ici les démonstrations de ces théorèmes. Ce sont des fichier PDF compressés en zip (si vous ne possédez pas le logiciel Acrobat Reader ou Winzip, allez sur la page de liens) :
Thébault sans complexes (33 Ko)
Aubel sans complexes (95 Ko)
Avec les complexes (56 Ko)