Les barycentres ont de nombreuses propriétés intéressantes, par exemple ils sont « conservés » par certaines fonctions (si G est le barycentre de A1, ..., An pondérés par certains coefficients, alors f(G) est le barycentre de f(A1), ..., f(An) pondérés par les mêmes coefficients). Voyons comment et pourquoi ils sont apparus.
Tout part de ce qu'on appelle les formules de Leibniz. On considère un ensemble fini de couples (Ai, ki) où Ai est un point du plan et ki est un nombre réel. Le but est de calculer à partir d'un point M du plan le nombre f(M) défini par f(M) = k1MA12 + ... + knMAn2. Plus précisément, on voit que le calcul de ce nombre fait apparaître n fois le point M (donc ses coordonnées) et on voudrait qu'il apparaisse moins de fois, afin de faire moins de calcul à chaque fois. Voici comment on procède :
Si la somme des ki est nulle, alors on considère un point B du plan choisi au hasard. Alors :
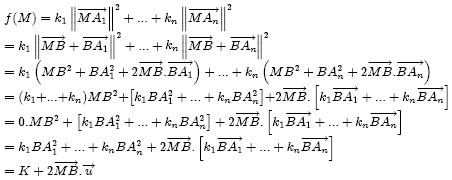
En effet, dans la dernière ligne du calcul, on voit que le nombre k1BA12 + ... + knBAn2 ne dépend pas de M et on le note K. De même, on a à droite un vecteur indépendant de M et on le note u. Ainsi, on peut calculer K et u une bonne fois pour toute ; le calcul de f(M) se réduira ensuite à un produit scalaire et une addition : M n'apparaît plus qu'une fois dans la formule !
Si la somme des ki est non nulle, on peut montrer qu'il existe un point G tel que 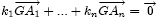 (c'est en fait une simple résolution d'équation du premier degré). Et alors, on a :
(c'est en fait une simple résolution d'équation du premier degré). Et alors, on a :
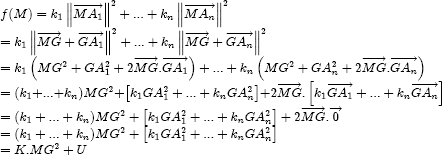
En effet, on fait apparaître de la même façon deux nombres indépendants de M qu'on peut calculer une fois pour toutes et M n'apparaît toujours qu'une fois !
Dans le deuxième cas, G est appelé barycentre des points pondérés (A1, k1), ..., (An, kn) et on voit son intérêt...