Vous vous rappelez ce qu'est le centre de gravité ? C'est l'intersection des médianes, ou si vous connaissez les barycentres c'est l'isobarycentre du triangle (pour plus de rappels sur les points particuliers du triangle, voyez Des médiatrices à la droite d'Euler).
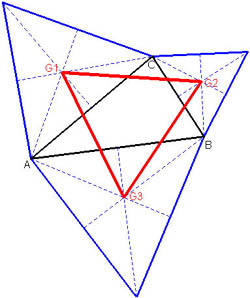Prenez à présent un triangle quelconque (ci-contre en noir). Sur chacun de ses trois côtés, on peut construire un triangle équilatéral extérieur (en bleu). Dans chacun de ces nouveaux triangles, on peut construire le centre de gravité (en rouge : G1, G2 et G3). On définit ainsi un dernier triangle G1G2G3.
Il se trouve alors que ce dernier triangle est toujours équilatéral, quelque soit le triangle de départ ! De plus, les deux triangles ont le même centre de gravité... Ce résultat peut se montrer en terminale avec les nombres complexes : cliquez ici (fichier PDF compressé en ZIP, 109 Ko. si vous n'avez pas Acrobat Reader ou Winzip, allez sur la page de liens).
Ce résultat est connu sous le nom de théorème de Napoléon, bien qu'il n'y ait aucune preuve tangible que l'empereur en soit bien l'auteur... De plus, il peut être vu comme le pendant dans un triangle du théorème de Victor Thébault (résultat semblable dans un quadrilatère).