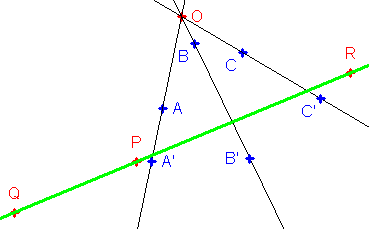
A partir de trois droites (ici en noir) (AA'), (BB') et (CC') concourantes en un point O, on réalise la construction suivante : Les droites (AB) et (A'B') se coupent en P (ici en rouge) ; (AC) at (A'C') en Q et (BC) et (B'C') en R. On constate alors que les points P, Q et R sont toujours alignés.
Il existe de nombreuses démonstrations de ce résultat, dont certaines sont très élégantes. Cependant, elles demandent des connaissances mathématiques assez élevées et je ne les présenterai donc pas ici. Ce qui m'intéresse est plutôt de vous montrer ce résultat intéressant mais aussi ce qu'il y a autour.
D'abord, sachez que s'il se démontre directement, il peut aussi être considéré comme conséquence du théorème de Pappus, qui parle également d'alignements de points créés par intersections d'autres points supposés alignés. En fait, c'est le cas de nombreux théorèmes de ce qu'on appelle la géométrie projective (voir plus bas), discipline due justement à Desargues.
Ainsi, le théorème de Desargues est intéressant pour son lien avec la géométrie projective. Mais il a un autre intérêt : si vous faites des recherches sur le sujet, vous trouverez de nombreuses autres formulations du théorème. C'est parce qu'il est également possible d'énoncer sa réciproque. On dit que c'est un théorème auto-dual.
Si vous voulez en savoir plus, je vous conseille http://igd.univ-lyon1.fr/~germoni/desargues/desargues1.html, qui propose une très belle démonstration du théorème, ou l'article de Wikipédia qui traite des différentes implications du théorème et survole plusieurs démonstrations différentes.
Mais qu'est-ce que la géométrie projective ?
En gros, elle consiste à établir une bijection entre des droites et des points, en utilisant des principes de perspective. Une nouvelle fois, je ne m'aventure pas dans des considérations trop difficiles (là encore, si vous en voulez plus, l'article de Wikipédia est très intéressant - non, je n'ai pas d'actions dans leur société !) mais je préfère insister sur son importance : la géométrie projective contient la géométrie plane. Elle est donc une sorte de généralisation de la géométrie euclidienne. Ainsi, de nombreux théorèmes (comme justement Desargues) qui se démontrent difficilement en géométrie plane se révèlent très simples en géométrie projective, devenant alors des cas particuliers d'autres théorèmes !
A propos, vous pouvez consulter la biographie de Jean-Victor Poncelet, le mathématicien qui a permis au XIXème siècle de redécouvrir cette géométrie auparavant oubliée.
Source :
http://www.univ-lyon1.fr