La relation ci-dessous a longtemps été appelée relation d'Euler car ce dernier l'a formulée en 1752. Cependant, on a découvert plus tard que Descartes avait démontré une formule équivalente dans un ouvrage qu'il n'avait pas publié. La formule est donc souvent nommée théorème de Descartes-Euler.
La formulation d'Euler dit que si l'on considère un polyèdre sans trou (en gros, cela signifie qu'il a toutes ses faces), ce qui est par exemple le cas des polyèdres connexes, et si on note respectivement f, a et s le nombre de faces, d'arêtes et de sommets du polyèdre, alors f - a + s = 2. Autrement dit, ces trois nombres sont liés dans la mesure où si vous en choisissez deux, vous imposez le troisième.
La formulation de Descartes dit qu'en considérant que l'angle droit est l'unité de mesure des angles (autrement dit, « un angle de 3 » signifie un angle de 270°), la somme des angles de toutes les faces d'un polyèdre convexe vaut 4(s-2). Les deux formulations sont bien équivalentes : si un polygone (dans un plan) a n côtés, alors la somme de ses angles vaut 2n - 4 (pour montrer cela, on découpe le polygone en n triangles se basant sur les côtés ; la somme des angles des triangles vaut alors 2n, car pour chacun la somme vaut 2, et il faut enlever 4 car on a rajouté au centre du polygone des angles qui ne devraient pas compter). On somme ce nombre, 2n - 4, pour toutes les faces du polyèdre. Il y en a f donc la somme des (-4) vaut -4f. La somme des 2n vaut deux fois la somme des n. Or la somme des nombres de côtés de chaque face vaut deux fois le nombre d'arêtes (puisque chacune est comptée deux fois) donc la somme des 2n vaut 4a. Ainsi la somme des 2n - 4, c'est-à-dire la somme des angles du polyèdre, vaut 4a - 4f. La formulation de Descartes dit donc en réalité que 4(a-f) = 4(s-2), ce qui est bien équivalent à la relation d'Euler.
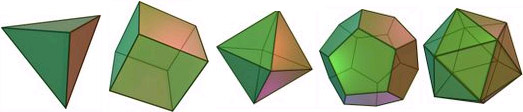Pour la démonstration du théorème, je vous renvoie à l'encyclopédie Wikipédia. Nous pouvons aussi vérifier la formule pour les cinq polyèdres de Platon (il existe seulement neuf polyèdres réguliers, c'est-à-dire dont toutes les faces sont identiques et forment des polygones réguliers, et dont les sommets sont identiques ; cinq d'entre eux sont convexes et sont dits platoniciens). De gauche à droite sur la figure :
- Le tétraèdre régulier est composé de triangles équilatéraux : f = 4, s = 4, a = 6.
- Le cube (ou hexaèdre) est composé de carrés : f = 6, s = 8, a = 12.
- L'octaèdre régulier est composé de triangles équilatéraux : f = 8, s = 6, a = 12.
- Le dodécaèdre est composé de pentagones : f = 12, s = 20, a = 30.
- L'icosaèdre est composé de triangles équilatéraux : f = 20, s = 12, a = 30.
Dans les cinq cas, on a bien f - a + s = 2 !
Une propriété semblable : Clous et polygones.
Sources :
Wikipédia