De nos jours, on apprend en primaire à poser une division. Mais à une époque, on apprenait aussi à calculer les racines carrées à la main ! Voici donc comment faire si vous n'avez pas de calculatrice.
1 - Description de l'algorithme
2 - Exemples
3 - Preuve de l'algorithme
4 - Les bâtons de Napier
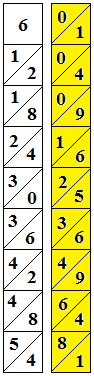Ces bâtons ont été inventés en 1617 par l'écossais John Napier, déjà inventeur du logarithme (d'où le nom de logarithme néperien). Ils facilitent le calcul de la racine carrée. Ces bâtons sont des colonnes ayant 9 cases. Pour les dix bâtons de base, on trouve en haut un chiffre et dans les huit cases en dessous sa table de multiplication : on trouve le résultat de ce chiffre multiplié par 2, puis 3, jusqu'à 9. Dans chaque case, le résultat contient 2 chiffres (si nécessaire on rajoute un 0) : la case est donc séparée en deux morceaux, un pour les dizaines et un pour les unités, sur le même principe en fait que la multiplication par jalousies (lisez cette page pour comprendre le principe des cases et des retenues). Par exemple ci-contre (en blanc), vous voyez le bâton 6. Il faut leur rajouter un bâton spécial (ci-contre en jaune), de 9 cases également, contenant de la même manière les carrés des 9 chiffres (sauf 0).
Et voilà à quoi ils servent. L'étape la plus calculatoire dans notre algorithme est de trouver, ayant un certain nombre M et un reste r, le plus grand chiffre x tel que Mx fois x soit inférieur à r. Et bien avec les bâtons, les multiplications sont toutes faites ! Par exemple, dans le premier exemple ci-dessus, il fallait à une étape trouver le plus grand x tel que 702a x a soit inférieur à 25500. Pour cela (illustration ci-dessous), on utilise les bâtons 7, 0 et 2 pour former en haut le nombre 702. Puis on juxtapose à droite le bâton spécial. On voit alors apparaître sur les 9 lignes les produits 7021 x 1, 7022 x 2, jusqu'à 7029 x 9. Par exemple, on n'a plus qu'à ajouter les retenues sur la ligne 6 pour lire que 7026 x 6 = 42156. Et donc, il n'y a plus qu'à lire chaque ligne pour trouver le plus grand résultat inférieur à 25500 !
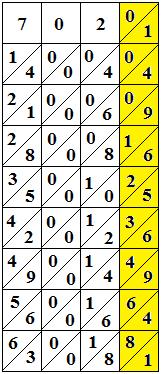Evidemment, il faut avoir plusieurs exemplaires de chaque baguette 0 à 9 (au cas où un chiffre se répèterait dans le nombre M), mais une seule baguette spéciale est nécessaire.
Source :
Des trucs et des maths