Voici une parabole très pratique :
Sur du papier quadrillé, construisez la parabole d'équation y = x². Indiquez sur la courbe tous les points d'abscisse entière. En légende, marquez à côté de chaque point les valeurs absolues des abscisses. Pour finir, graduez l'axe des ordonnées (seulement les points d'ordonnée positive) à chaque point d'ordonnée entière et indiquez le chiffre correspondant.
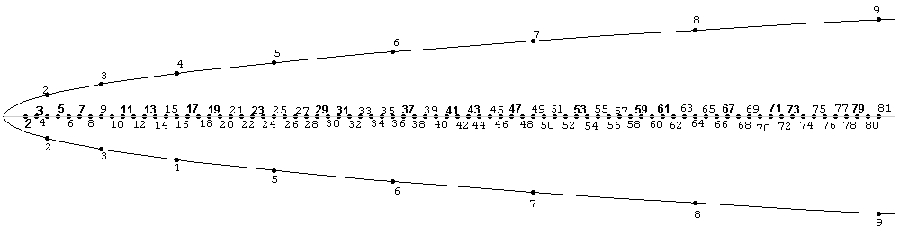
(sur cette image, j'ai inversé abscisse et ordonnée.)
A quoi sert-elle ?
Pour multiplier deux nombres a et b, prenez sur la partie gauche de la parabole le point noté a et sur la partie droite le point marqué b. Tracez la droite reliant les deux points. Regardez le point d'intersection avec l'axe des ordonnées : l'ordonnée de ce point est le produit de a et b.
D'accord, pour calculer 8x6, c'est franchement inutile. Mais si vous n'avez pas de calculette à portée de main pour calculer 8,5 x 4,2, c'est plus rapide que faire le calcul à la main. Mais attention, celà ne donne qu'une valeur approchée (la lecture du résultat est sujette à l'imprécision de la mesure).
Pourquoi ça marche ?
Reprenons nos deux nombres a et b. Vous avez choisi sur la courbe les points d'abscisse respectives -a et b. Ils ont donc pour coordonnées respectives (-a ; a2) et (b ; b2). Cherchons l'équation de la droite reliant les deux points :
Son équation est de la forme y = mx + p. Or les points de coordonnées (-a ; a2) et (b ; b2) obéissent à cette équation. D'où : a2 = -am + p et b2 = bm + p.
Il s'agit de résoudre le système formé par ces deux équations pour trouver m et p. Par soustraction de la première à la deuxième, on a :
b2 - a2 = (b + a)m donc m = (b2 - a2)/(b + a) = (b + a)(b - a)/(b + a) = b - a.
On reporte cette expression dans une des deux équations et on trouve : p = ab.
L'équation de la droite est donc : y = (b - a)x + ab.
Il ne reste plus qu'à calculer l'ordonnée du point d'intersection avec l'axe des ordonnées : l'abscisse étant 0, l'ordonnée vaut ab.