De nos jours, on apprend en primaire à poser une division. Mais à une époque, on apprenait aussi à calculer les racines carrées à la main ! Voici donc comment faire si vous n'avez pas de calculatrice.
1 - Description de l'algorithme
2 - Exemples
3 - Preuve de l'algorithme
4 - Les bâtons de Napier
Voici deux exemples. Dans le premier, nous cherchons la racine carrée de 123456. On commence par le séparer en tranches de 2 chiffres :
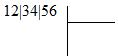
On cherche le plus grand carré inférieur à 12 : c'est 32 = 9. On inscrit donc 3 en haut à droite, et on soustrait au 12 le carré 9, ce qui donne un reste de 3. On inscrit ce 3 en dessous de 12 et on abaisse la tranche 34 :

Le début de la racine étant 3, on double ce nombre pour trouver 6. Nous devons donc trouver le plus grand a tel que 6a x a soit inférieur 334. Il s'agit de 5. On inscrit donc 5 à côté du 3 (deuxième chiffre de la racine), et on soustrait à 334 le produit 65 x 5, ce qui donne un reste de 9. On abaisse la tranche 56 :
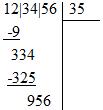
Le début de la racine étant 35, on double ce nombre pour trouver 70. Nous devons donc trouver le plus grand a tel que 70a x a soit inférieur 956. Il s'agit de 1. On inscrit donc 1 dans la racine, et on soustrait à 956 le produit 701 x 1, ce qui donne un reste de 255 :
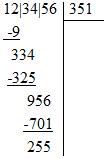
Si l'on ne veut que la partie entière de la racine, on a terminé : elle vaut 351. Plus précisément, on a 123456 = 3512 + 255. Cependant, on peut aussi choisir de continuer l'algorithme pour avoir les décimales. On ajoute donc une virgule à la racine et on abaisse une tranche de zéros :
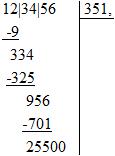
Le début de la racine étant 351, on double ce nombre pour trouver 702. Nous devons donc trouver le plus grand a tel que 702a x a soit inférieur 25500. Il s'agit de 3. On inscrit donc 3 dans la racine, et on soustrait à 25500 le produit 7023 x 3, ce qui donne un reste de 4431 :
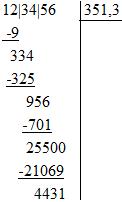
La première décimale de la racine carrée de 123456 est donc 3... on peut continuer cet algorithme à l'infini en abaissant des zéros (je vous laisse vérifier que la décimale suivante est 6).
Voici un autre exemple, qui lui se termine sur une valeur exacte (et entière). On calcule ainsi à la main que la racine carrée de 1456849 est 1207 :
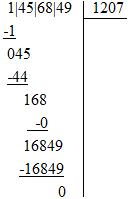
Source :
Des trucs et des maths