Soit un cercle de centre O et de rayon R et un point A quelconque du plan. Tracez une droite passant par ce point et qui coupe le cercle en deux points B et C. Alors nous allons étudier le produit AB.AC (distances orientées).
I) Que pouvez-vous dire du signe de ce produit selon la position de A ?
Si A est à l'intérieur du cercle, AB et AC sont de signes opposés donc le produit est négatif. Si A est à l'extérieur, AB et AC sont de même signe donc le produit est positif. Si A est sur le cercle, l'un des deux points B et C est confondu avec A donc le produit est nul. On voit donc que le signe ne dépend pas de la droite choisie.
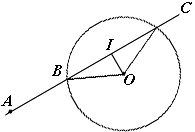II) En fait, le produit lui-même est indépendant de la droite choisie. Exprimez sa valeur en fonction de R et de la distance OA (non orientée). On appelle cette valeur puissance du point A par rapport au cercle.
Remarque : dans la suite, on notera les vecteurs avec une simple barre au-dessus des deux lettres (exemple : AB)
Soit P(A) le produit cherché et I le milieu de [BC]. P(A) = AB.AC = (AO + OB).(AO + OC) = AO2 + AO.OC + OB.AO + OB.OC = AO2 + AO.(2OI) + OB.OC
Or OB.OC = (OI + IB).(OI + IC) = OI2 + OI.IC + IB.OI + IB.IC = OI2 + IB.IC = OI2 - IB2
Donc P(A) = AI2 + OI2 + AO.(2OI) + OI2 - IB2 = AI2 + 2OI2 + 2AO.OI - IB2 = AI2 + 2OI.AI - IB2 = AI2 - IB2
D'après le théorème de Pythagore, P(A) = AO2 - OI2 - IB2 = AO2 - OB2 = AO2 - R2.
On peut vérifier que le signe de ce nombre est en accord avec la première remarque.
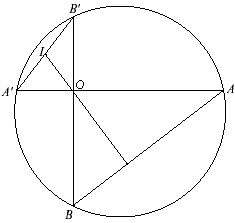III) Une application
Soit un cercle et un point O dans ce cercle. On construit deux droites perpendiculaires passant par O ; une des droites coupe le cercle en A et A', l'autre en B et B'. Pourriez-vous démontrer que la médiane issue de O dans le triangle A'OB' est aussi la hauteur issue de O dans le triangle OAB ? On note I le milieu de [A'B'] et on calculera AB.OI en trouvant d'abord une relation simple entre OI, OA' et OB'.
Solution