Je vous propose de refaire vous-même l'une des nombreuses démonstrations du théorème de Pythagore (qui ne serait d'ailleurs pas du à Pythagore !) grâce à mes indications.
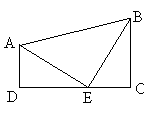Sur cette figure, les triangles ADE et BEC sont identiques, l'un étant obtenu à partir de l'autre par une rotation d'angle 90°. ADE est rectangle en D ; BEC est rectangle en C. Enfin, les points D, E et C sont alignés.
On donne AD = a ; DE = b ; AE = c.
Comme les triangles ADE et BEC sont identiques, les angles (désolé, je ne mets pas les chapeaux pour des raisons de facilité) AED et EBC sont égaux. On a donc la relation sur les angles : AED + BEC = EBC + BEC = 90°. Or on a aussi AED + AEB + BEC = 180° (D, E, C alignés) et on en déduit AEB = 90° Le triangle AEB est rectangle en E. De plus puisque ADE et BEC sont identiques, AE = EB donc AEB est rectangle isocèle en E.
En déduire la surface du quadrilatère ADCB.