« Savoir que la 293ème décimale du nombre pi est un 7 ne m'intéresse pas. Mais savoir quel est le raisonnement ou la méthode qui a permis de la trouver, voilà qui m'intéresse davantage. » (Albert Jacquard, Sciences et avenir 674, avril 2003)
Calcul de pi avec les séries
Une série est une somme ayant un nombre infini de termes. Bien sûr pour que cela ait un sens, il faut qu'en sommant peu à peu tous les termes, on obtienne une valeur limite finie. Par exemple, on peut considérer la somme des puissances de 1/2 : 1 + 1/2 + 1/4 + 1/8 + ... En effet, en sommant les termes peu à peu, on obtient les sommes intermédiaires 1 puis 3/2 puis 7/4 puis 15/8, etc... On démontre que ces sommes intermédiaires tendent vers 2, ce qui justifie que la « somme infinie » (la série) existe et vaut 2. En revanche, on ne peut pas définir la série 1 + 1 + 1 + 1 + ... car les sommes intermédiaires valent 1, 2, 3, 4, ... et ne tendent pas vers un nombre fini.
Ainsi si on arrive à prouver qu'une série tend vers un certain nombre, alors plus on sommera de termes de cette série, plus on obtiendra une valeur proche du nombre en question... Une application est de calculer pi. Voici quelques séries qui permettent de le faire (mais il existe bien d'autres).
Dans la formule ci-dessous, n est un angle en degrés. Il est alors astucieux de choisir n = 45°, car tan(45°) = 1 et on obtient la deuxième formule. Avec cette deuxième formule, en sommant les termes jusqu'à 1/17, on obtient pour valeur approchée de pi 3,252365935 (écart de 3,53 % avec la valeur exacte).
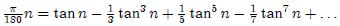
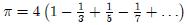
Cette autre formule est due à Jacques Bernoulli. En faisant le calcul jusqu'à la dixième fraction, on approche pi par la valeur 3,049361636 (écart de 2,94 %).
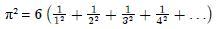
Le dernier exemple ci-dessous demande plus de calcul, mais en allant seulement trois fractions plus loin, on trouve l'approximation 3,137129537 (écart de seulement 0,14 %).
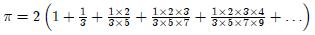
Calcul de pi par les probabilités :
Notons x la valeur de pi. On dispose d'un plancher composé de lames de largeur a. On lance sur ce plancher N aiguilles de longueur b. Si N est assez grand, on peut considérer que toutes les aiguilles sont orientées différemment. Elles forment alors un polygone à N côtés et de périmètre Nb. On peut donc approcher ce polygone par un cercle de diamètre Nb/x. Le diamètre du cercle chevauche alors deux lames en Nb/ax points. Notre polygone chevauche donc deux lames en 2Nb/ax points. Autrement dit, 2Nb/ax aiguilles chevauchent deux lames.
Soit P la probabilité qu'une aiguille chevauche deux lames. On a alors P = 2b/ax. Si on réalise l'expérience avec des aiguilles dont la longueur est la largeur des lames (a = b), on a P = 2/x d'où x = 2/P.
L'expérience donne par exemple (je ne l'ai pas faite moi-même) P = 0,6366666 d'où pi = 3,141361289438 (écart de 0,007 %).
Voir aussi : les décimales de pi
Sources :
Calcul de pi avec les séries : Les nombres et leurs mystères, André Warusfel, éditions du Seuil, 1961
Calcul avec les probabilités : Palais de la Découverte, Paris.