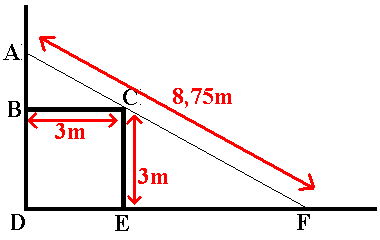
On nommera d la distance DF et h la hauteur AD.
Première étape
On a ici trois moyens d'arriver au même résultat. Le premier est le théorème de Thalès : Comme (BC) est parallèle à (DF), on a AB/AD = BC/DF ce qui donne (h-3)/h = 3/d ou 3h + 3d - dh = 0.
Le deuxième est l'utilisation des triangles semblables ABC et CEF : on a AB/BC = CE/EF ce qui donne (h-3)/3 = 3/(d-3) ou (h-3)(d-3)=9. Après simplification, on retrouve 3h + 3d - dh = 0.
Enfin, on peut calculer l'aire du triangle ADF : elle vaut ADxDF/2 = hd/2. Mais c'est aussi la somme des aires du carré BCED (3x3 = 9), du triangle ABC (ABxBC/2 = 3(h-3)/2) et du triangle CEF (CExEF/2 = 3(d-3)/2). On a donc :
hd/2 = 9 + 3(h-3)/2 + 3(d-3)/2 soit hd = 3h + 3d.
Deuxième étape
Il faut donc trouver une autre relation entre h et d. Nous n'avons pas utilisé la longueur de l'échelle. Il faut donc le faire ici avec le théorème de Pythagore : AD2 + DF2 = AF2, c'est-à-dire h2 + d2 = 8,752 = 76,5625.
Troisième étape
Nous devons maintenant simplifier ces relations. Soit P = hd et S = h + d. On a 3S - P = 0 et h2 + d2 = 76,5625. La deuxième relation donne (h+d)2 = h2 + d2 + 2hd = 76,5625 + 2hd. Ce qui revient à S2 = 76,5625 + 2P. Or 3S - P = 0 donc P = 3S et, en remplaçant, S2 = 76,5625 + 6S. C'est une équation du second degré dont les deux solutions sont : -6,25 et 12,25. Or h et d sont des distances. Ce sont donc des nombres positifs. S est donc aussi positif, on en déduit S = 12,25. Comme P = 3S, on a P = 36,75. Ainsi, h+d = 12,25 et hd = 36,75.
Résolution
h et d sont donc les deux solutions de l'équation :
x2 - 12,25 x + 36,75 = 0. (si vous ne voyez pas pourquoi, cliquez ici). Ils valent donc 5,25 et 7.