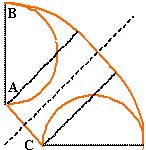
 Vu les données du problèmes, on peut placer les points A, B et C comme ci-contre et comprendre la construction de l'arbalète : on a construit le demi-cercle de diamètre [AB] puis on a commencé le cercle de centre A et passant par B jusqu'à former un angle de 45° (ce qui fait donc un huitième de cercle). Sur l'autre rayon de ce huitième de cercle, on a construit le rectangle avec pour autre côté AC et enfin on a complété la figure par symétrie axiale, d'axe la médiatrice de [AC].
Vu les données du problèmes, on peut placer les points A, B et C comme ci-contre et comprendre la construction de l'arbalète : on a construit le demi-cercle de diamètre [AB] puis on a commencé le cercle de centre A et passant par B jusqu'à former un angle de 45° (ce qui fait donc un huitième de cercle). Sur l'autre rayon de ce huitième de cercle, on a construit le rectangle avec pour autre côté AC et enfin on a complété la figure par symétrie axiale, d'axe la médiatrice de [AC].
Ainsi l'aire de l'arbalète est l'aire du huitième de cercle, multipliée par 2 puisqu'il y a le morceau symétrique, plus l'aire du rectangle, en retranchant au tout l'aire du demi-cercle, multipliée par 2 elle aussi. C'est donc 2 fois l'aire d'un huitième de disque de rayon 20 plus l'aire d'un rectangle de côtés 20 et 10 moins 2 fois l'aire d'un demi-disque de diamètre 20, soit encore l'aire du quart d'un disque de rayon 20, plus 200, moins l'aire d'un disque de rayon 10.
Le calcul donne 20*20*pi/4 + 200 - 10*10*pi = 200 cm2 exactement.