On ne connaît pas le rayon du petit cercle, donc puisque les indications du document sont suffisantes, cela signifie que le rayon du petit cercle n'a pas d'importance. On peut donc le choisir, et par exemple le prendre nul : alors la distance AB est un diamètre de l'arène qui est entièrement occupée par les gradins. La surface de ceux-ci est donc celle d'un cercle de rayon 50 perches, soit environ 7854 perches-carrées.
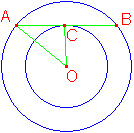Si vous n'êtes pas convaincu(e) par ce raisonnement, en voici un plus compliqué mais plus classique. On note O le centre de l'arène et C le point où [AB] touche le cercle. Alors le rayon de l'arène vaut OA et le rayon de la piste vaut OC. L'aire des gradins est donc celle de l'arène moins celle de la piste, soit OA2pi - OC2pi = (OA2 - OC2)pi. Or le théorème de Pythagore donne OA2 - OC2 = AC2 = 502, et on retrouve 7854.